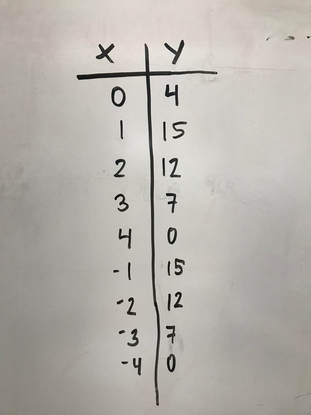Problem Statement
A rectangle has one corner on the graph of y=16-x^2 another at the origin, a third on the positive y axis and the fourth on the positive x axis.
If the area of the rectangle is a function of X, what value of x yields the largest area for the rectangle
If the area of the rectangle is a function of X, what value of x yields the largest area for the rectangle
Process
My initial attempt was to factor the equation, but I soon realized that this was an equation that could be graphed so I didn't need to or we couldn't. So we started an X,Y table and started plotting points for X in the equation y=16-x^2 to find the value for Y and we were able to graph it.
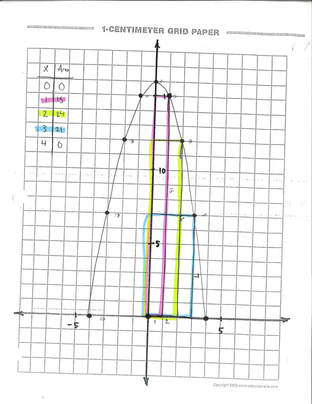
Here are the plots we got when plugging X values to find Y and the end result after plotting them on the graph.
Solution

Maximun Area
When finding areas for rectangle we knew that we needed to multiple the length and width so in that case we multiplied X and Y to get the area of the rectangles. The general formula that we used to find the area was
X(16-x^2) = Area
We realized that this wouldn't be the maximum area of the rectangle and that we could go into the decimals. So we looked at what the biggest area was given those points and we saw that it was between 2 and 3 so we knew that we could plug in decimal points around those numbers. We knew to check numbers like 1.9, 2.1, 2.2, 2.3 and so on until we found the highest one.
We realized then that we could continue to go further and further to find the maximum area of the rectangle by continuing the decimals but because it is in irrational number the number will be irrational so the method guessing and checking will just continue. The way you would find the exact number is by calculus. The number we stopped at was the nearest tenth and the maximum area that we got was.......
X= 2.1
A = gives your largest area but, not exact
Maximum Perimeter
For the maximum perimeter we knew that we had to add all the sides together and we were able to come up with general formulas for perimeter like...
2w+2l = perimeter
2(w+l) = perimeter
with the same x, y table we just started to plug those into the formulas. X would be the width, and l would be the length so we just plugged those into the formulas. A more generic formula for this specific equation is 2x + 2(16-x^2) = perimeter Once we plugged it in and got a feel for where the maximum perimeter was going to be we then when further into decimal points and found that the answer was
X= ..5
P= 32.5
When finding areas for rectangle we knew that we needed to multiple the length and width so in that case we multiplied X and Y to get the area of the rectangles. The general formula that we used to find the area was
X(16-x^2) = Area
We realized that this wouldn't be the maximum area of the rectangle and that we could go into the decimals. So we looked at what the biggest area was given those points and we saw that it was between 2 and 3 so we knew that we could plug in decimal points around those numbers. We knew to check numbers like 1.9, 2.1, 2.2, 2.3 and so on until we found the highest one.
We realized then that we could continue to go further and further to find the maximum area of the rectangle by continuing the decimals but because it is in irrational number the number will be irrational so the method guessing and checking will just continue. The way you would find the exact number is by calculus. The number we stopped at was the nearest tenth and the maximum area that we got was.......
X= 2.1
A = gives your largest area but, not exact
Maximum Perimeter
For the maximum perimeter we knew that we had to add all the sides together and we were able to come up with general formulas for perimeter like...
2w+2l = perimeter
2(w+l) = perimeter
with the same x, y table we just started to plug those into the formulas. X would be the width, and l would be the length so we just plugged those into the formulas. A more generic formula for this specific equation is 2x + 2(16-x^2) = perimeter Once we plugged it in and got a feel for where the maximum perimeter was going to be we then when further into decimal points and found that the answer was
X= ..5
P= 32.5
Group Test/ Individual Test
Our group studied for the math test by doing the practice problem that Mr. B gave us and we reviewed the notes that we took from the first problems we did. During the actual group quiz my table got into little funk where we had separate ideas of how to approach the problem and so we spent a lot of the class time overthinking the problem. I wouldn't say that I felt negative but, more lost and confused and feeling like making no progress. Spending most of the class time on debating on how to approach the problem we only had 5 minutes for the individual test and I felt good about it. Overall experience of the group quiz was a big learning moment, I don't see our group as feeling negative but, more of challenging each other. We all struggled together,
Evaluation/ Reflection
This unit pushed my thinking in making sure to ask clarifying questions. The way our group handled the problem wasn't that one person was leading and doing all the work we were all pushing each other to explain why they think what they think and pushed each other to provide and evidence and reasoning which I was a good think, but the problem was that we all didn't know how to come to an agreement because our strategies to approach the problem were all so different. I think if I were to grade myself this unit I would give myself an A+ because I did understand the subject well and I did what I could to help other peers when they were struggling.