Problem Statement
|
The rules of the California Super Lotto are
1. Chose any 5 number between 1-47 (these numbers will not repeat) 2. Pick a mega number between 1-27 (this number may repeat) 3. Match all 5 numbers and the mega number and you win The problem we are trying to solve is 1. How many different number combinations are possible for a CA Super Lotto ticket? 2. What is the probability of winning the CA Super Lotto? 3. If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings? |
Process and Solution
1. How many different number combination are possible for a CA Super Lotto ticket?
Immediately looking at this problem I knew to look at the past problem we did called "Mr. B's Closet" It had a similar problem where we had to calculate the total combinations of different outfits he could make. We took all the pairs of Shirts, shoes, socks, and ties and multiplied them all to get the total amount of combinations. So we applied that to our Super Lotto problem.
Immediately looking at this problem I knew to look at the past problem we did called "Mr. B's Closet" It had a similar problem where we had to calculate the total combinations of different outfits he could make. We took all the pairs of Shirts, shoes, socks, and ties and multiplied them all to get the total amount of combinations. So we applied that to our Super Lotto problem.
Initial attemptThis was my initial thought. The reason why the denominators are decreasing is because one of the rules is that the numbers can't repeat therefor the sample space gets smaller and smaller. Once we got all 6 spots including the mega number we multiplied and got the number 4,969,9962,360 SolutionWe had the right idea to multiply but the thing we were missing is that since there are 5 spots.. We have to decrease those spots as well. So the total combinations possible are
120/4,969,9962,360 |
|
2. What is the probability of winning the Super Lotto?
Initial Thought At the beginning of the unit my original guess was that one in one million people who win the super lotto. I was way off. Solution Solving for the total combinations basically gave us the answer to this problem. We have .. 120/4,969,9962,360 and when we simplify we get = 1/41,416,353 One in forty one thousand four hundred sixteen thousand three hundred fifty three chance in winning the California Super Lotto. When divided and put in percentages equals .00000000241 = 0% |
3. If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
Initial Attempt
Initially we used the formula to calculate our expected value, but one mistake we made was that I thought that the winnings was $8,000 dollars instead of $8,000,000, so that messed up our whole answer and we had to start the whole process over again.
Initially we used the formula to calculate our expected value, but one mistake we made was that I thought that the winnings was $8,000 dollars instead of $8,000,000, so that messed up our whole answer and we had to start the whole process over again.
Problem EvaluationI actually really liked this problem. I thought that it was fun and it made sense. I think the most I got out of this problem was the reality of winning the super lotto. Doing the numbers and calculating the probability I feel, opens your eyes more to how unlikely you are to win.
|
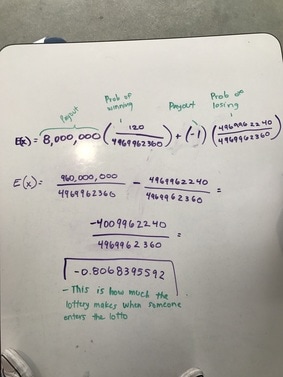
SolutionWe followed the rule Mr. Carter gave us for expected value. Thats why on the picture you see the $8 million dollars for as a payout and the probability of winning that money. The next thing can happen is that your betting $1 and then you multiply that by the probability of losing. When you solve it out completely you get the decimal.
-0.8068395592 which, when rounded is 81 that tells us that the lottery makes 81 cents every time someone pays a dollar to enter the lotto. In the long run the lotto is making lots of money because people continue to buy the lotto when in reality they have a 0% chance of winning. |
Self EvaluationIf I were to grade myself on this unit I would give myself an A+. I was focused during class, I stayed on task, whenever I felt lost I made sure to answer questions. I did my best to work towards my goal, which was to work with my group. I constantly checked in on everyone making sure they knew what they were doing.
|
Challenge Option
The challenge option that we chose to take on was that at one point when they continue to raise the payout price does the expected value actually start to be profitable for you. How much would the payout have to be?
The first thing we did was to increase the payout by two million. We decided to keep a table to keep track of our payout and expected value. What we found was that every time we increase the payout by two million the expected value would decrease by 5.
The first thing we did was to increase the payout by two million. We decided to keep a table to keep track of our payout and expected value. What we found was that every time we increase the payout by two million the expected value would decrease by 5.
As soon as we realized that pattern, we knew that we needed to get the expected value to equal to 0 because that would mean that for every time someone entered the lotto the lotto would not make a profit.
We found that when you raise the payout to $20,000,000 you get an expected value around 51 cents. Since we needed that 51 cents to get to zero and we knew that 5 decreased the expected value every time you raise the payout. We decided to subtracts the 51 by 50 adding a zero, so that meant we had to increase the payout by 20 million more. Which gave us
Payout = $40,000,000 we checked the expected value by plugging in the payout in our expected value formula.
Expected Value = 3 cents.
This still didn't get us to 0 cents and so we raised the payout very little since we close to zero. So we tried
Payout = $41,000,000
Expected Value = 1 cent
Still that didn't get us to zero but that was very close. So we raised it again but only slightly.
We found that when you raise the payout to $20,000,000 you get an expected value around 51 cents. Since we needed that 51 cents to get to zero and we knew that 5 decreased the expected value every time you raise the payout. We decided to subtracts the 51 by 50 adding a zero, so that meant we had to increase the payout by 20 million more. Which gave us
Payout = $40,000,000 we checked the expected value by plugging in the payout in our expected value formula.
Expected Value = 3 cents.
This still didn't get us to 0 cents and so we raised the payout very little since we close to zero. So we tried
Payout = $41,000,000
Expected Value = 1 cent
Still that didn't get us to zero but that was very close. So we raised it again but only slightly.
Peer Critiques
Celebrations
"Easy to read" - Alexandra
"Clear pictures" - Alexandra
"Great Examples" - Alexandra
"I like how you typed the number out" - Trinity
" I like your lottery picture" - Trinity
" I like your header" - Trinity
"Clear pictures" - Alexandra
"Great Examples" - Alexandra
"I like how you typed the number out" - Trinity
" I like your lottery picture" - Trinity
" I like your header" - Trinity
Feeback
"Add a picture of the challenge problem" - Trinity
"Try to make some of the picture bigger you can see them better" - Alexandra
"Show the math for the challenge option" - Alexandra
"Try to make some of the picture bigger you can see them better" - Alexandra
"Show the math for the challenge option" - Alexandra
Revisions
- I made some of the pictures bigger
- Revised grammar
- Added pictures
- Rephrased some of my paragraph so that it makes more sense