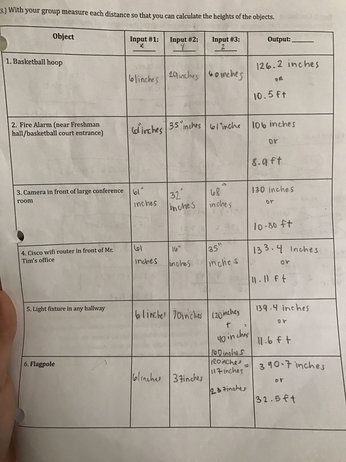
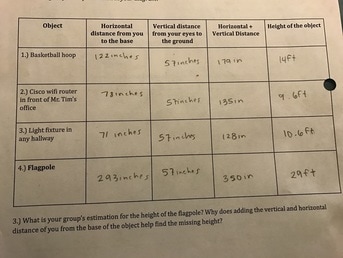
Problem Statement
High Tech High Chula Vista is trying to get a new flag for the flagpole, but requires to know the height. Our job was to use different methods, and to set up proportion to solve for the height, without having to actually measure the flagpole itself.
Process and Solution
At the beginning of this unit. Everyone took an initial estimate of the flagpole. My estimation was that the flagpole had a minimum height of 25ft and a maximum of 30ft. I knew my height was 5'1 so I imagined how many times would I have to stack myself up to reach the flagpole. I thought maybe 5 or 6 times.
Similarity: Similarity it is the same shape but different size. In order for shapes to be similar they have to have equal corresponding angles. When they have the corresponding equal angles that means that the shapes are the same. Once you have the same angles, in order for them to be a different size they have to be proportional.
Shadow Method
For this method we used shadows to help us set up proportions to find the height of the flagpole. By comparing the height of a person, and their shadow versus the shadow of the flagpole we were able to create triangles, and a proportion.
Similarity: Similarity it is the same shape but different size. In order for shapes to be similar they have to have equal corresponding angles. When they have the corresponding equal angles that means that the shapes are the same. Once you have the same angles, in order for them to be a different size they have to be proportional.
Shadow Method
For this method we used shadows to help us set up proportions to find the height of the flagpole. By comparing the height of a person, and their shadow versus the shadow of the flagpole we were able to create triangles, and a proportion.
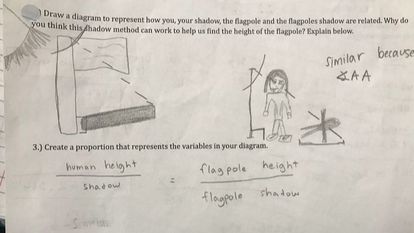 Diagram and proportion we set up
Diagram and proportion we set up
Before setting up proportions we needed to prove that the two triangles were similar. We found that the angle in which the sun comes down is one of the angles both triangles share. The second angle is the 90 degree angle both the flagpole and the person share. With the two angles, it was enough to prove they were both similar. This is what we called Angle Angle Theorem.
Once our group came up with a proportion and proved similarity we were able to plug in our specific measurements.
Proportion: Measurements:
Human Height = Flag Height |
|
Flagpole |
|
Sam |
Solution:
For our solution we plugged our measurements into the proportion we set up. For the flagpole height part of the proportion we left is as "x" because that's what we were finding. The final step was to cross multiply and solve for X. The height estimation that we eventually got using method was:
22ft
Mirror Method
For this method we measured the heights of objects by using a mirror. This method created triangles to help find set up proportions and find the height of the flagpole. This method created two triangles because, it begins by putting a mirror on the ground and you back up, looking at the object until to you see the object in your mirror.
For our solution we plugged our measurements into the proportion we set up. For the flagpole height part of the proportion we left is as "x" because that's what we were finding. The final step was to cross multiply and solve for X. The height estimation that we eventually got using method was:
22ft
Mirror Method
For this method we measured the heights of objects by using a mirror. This method created triangles to help find set up proportions and find the height of the flagpole. This method created two triangles because, it begins by putting a mirror on the ground and you back up, looking at the object until to you see the object in your mirror.
|
Before we went out to get our measurements we first set up variables in the triangle for a person's height, each distance, and for the height of the object. So that once we did get our measurements we could set up proportions and plug it in.
X = Height Y= Horizontal distance from person to mirror Z= Horizontal distance from object to mirror ?= Objects height After getting the measurements we needed we used our proportion, and plugged in to find the height. Y/Z = X/ ? After plugging our measurements for the flagpole and cross multiplying our final estimation using the mirror method was : 32.5ft Clinometer Method
Isosceles Triangles: An isosceles triangle is a triangle with two equal sides. With two equal sides comes two equal angles. What we did for this method to calculate the height of the flagpole was took a protractor with a straw on top of it and a piece of string and used that to find measurements of certain objects to find the height of the flagpole. This tool is used to measure the angle of elevation, or angle from the ground, in a right angled triangle. First we drew a diagram representing the right angled isosceles triangle including the flagpole and person, and then labeling it after. |
|
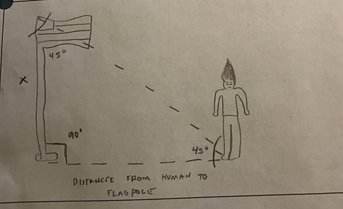
Soon after we took our clinometer tool, took our measurements and gather information. Secondly we added the horizontal distance + vertical distance to calculate the height of the object.
Which method do I think is most accurate?
I think that the most accurate method was the shadow method because I think that comparing the height and shadow of a person and setting up proportion was a more accurate way vs the rest of them. Each method got all nearly the same answer, so my final guess would probably 28 ft height since its average of all the methods.
Problem Evaluation
I didn't really enjoy this problem as far as our overall question but, I really enjoyed this unit. Our other overall question was something interesting. For example the chances of winning the lottery. This one knowing the height of the flagpole does not interest me. This whole unit of similarity, angles, proportion, and triangles was really fun though. Something that pushed my thinking was working in my group because its a hard unit to explain to someone because there are so many different rules, and theorems, so having to re-explain everything for them to understand why we did a certain step or why we solved it in a certain pushed me of thinking of how to explain it in a way they could understand.
Self Evaluation
If I were to grade myself for this unit I would grade myself an A+. This whole unit I was very engaged in what I was learning, and I was constantly working. Whenever Mr. C would show us a new way to come about the problem I would be actively listening and taking notes. I felt that this unit challenged me as well to prove why, for example before setting up proportions you have to prove why they are similar, after you set up proportions provide a justification, etc. So this unit I feel prepared me to be ready to answer why, for every decision we chose to solve a problem.
Edits
- Explain more how isosceles triangles apply
- Add something to fill negative space
-Make the headers the same colors
- Explain more of my though process for my initial estimation
- Add evidence to your self evaluation
- Add something to fill negative space
-Make the headers the same colors
- Explain more of my though process for my initial estimation
- Add evidence to your self evaluation